Posted on 2012-01-09 14:20
魔のkyo 阅读(3307)
评论(0) 编辑 收藏 引用

在空间直角坐标系中,计算对某个坐标轴的转动惯量公式:
Jxx = ∫rx2dm , Jxx表示绕x轴的转动惯量,rx为质量元到x轴的距离
Jyy = ∫ry2dm
Jzz = ∫rz 2dm’
平行轴定理:J=J0+md2
转动惯量张量(inertia tensor):
| J = | 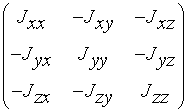 |
主对角线上为三个坐标轴的转动惯量,剩下的项称为惯性积(product of inertia):
Jxy = Jyx = ∫(xy)dm
Jyz = Jzy = ∫(yz)dm
Jzx = Jxz = ∫(zx)dm
惯性积也有类似平行轴定理的坐标轴转换公式:
Jxy = Io(xy)+mdxdy
Jyz = Io(yz)+mdydz
Jzx = Io(zx)+mdzdx
惯性积可能是正值也可能是负值,对于轴对称物体,如果选择对称轴为主轴,按照惯性积的定义,与对称轴有关的惯性积都为零。这极大地简化了惯性张量的计算,所以在物理模拟计算中一般就选取物体自身对称轴来生成local坐标系下的转动惯量张量。
由 T = Jβ ,T为扭矩,β为角加速度
两边乘以 J-1 得, J-1 T = β
由此可以通过扭矩得到角加速度。
但一般扭矩T的表示是在world坐标系下的,而前面说了惯量张量J的表示是在local坐标系下的,为了得到world坐标系下的β,我们可以先把扭矩变换到local坐标系,再用J-1 左乘之得到local坐标系下的角加速度,再将之变换到world坐标系下,即:
β = M J-1 M-1 T ,M为物体的worldTransform,事实上角加速度和物体的空间位置显然没有关系,所以其实M只需要表示出参照系的轴向即可,或者说只需要transform的旋转部分即可。
有了角加速度,我们便可以在物理模拟程序中计算出角速度在当前帧的增量
Δω = βΔt ,Δt为一帧的耗时。