1. 问题描述（贪心算法）
一个旅行家想驾驶汽车从城市A到城市B（设出发时油箱是空的）。给定两个城市之间的距离dis、汽车油箱的容量c、每升汽油能行驶的距离d、沿途油站数n、油站i离出发点的距离d[i]以及该站每升汽油的价格p[i],i=1,2,…,n。设d[1]=0<d[2]<…<d[n]。要花最少的油费从城市A到城市B，在每个加油站应加多少油，最少花费为多少？
2. 具体要求
Input
输入的第一行是一个正整数k，表示测试例个数。接下来几行是k个测试例的数据，每个测试例的数据由三行组成，其中第一行含4个正整数，依次为A和B两个城市之间的距离d1、汽车油箱的容量c（以升为单位）、每升汽油能行驶的距离d2、沿途油站数n (1<=n<=200)；第二行含n个实数d1, d2 ,…, dn，表示各油站离出发点的距离（d1=0）；第三行含n个实数p1, p2 ,…, pn，表示各油站每升汽油的价格。同一行的数之间用一个空格隔开。
Output
对于每个测试例输出一行，含一个实数，表示从城市Ａ到城市Ｂ所要花费的最少油费（输出的结果精确到小数点后一位）。若问题无解，则输出“No Solution”。
3. 测试数据
Sample Input
2
1500 50 10 4
0 300.0 800.0 1200.0
4.0 5.0 4.0 4.5
1000 40 10 3
0 500.0 750.0
4.5 5.0 4.2
Sample Output
640.0
No Solution
4．设计与实现的提示
（1） 注意考虑无解的情况
（2） 对终点站可进行特殊处理
5、代码实现（java）
1
/** *//**
2
* @(#)Ex5_1.java
3 *
4 *
5 * @author 叶云策（Intrl）
6 * @version 1.00 2009/4/17
7
*/
8
9import java.io.*;
10public class Ex5_1 
{
11 public static void main(String[] args) throws Exception
12
{
13 Ex5_1 intrl=new Ex5_1();
14 BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
15 System.out.println("请输入测试例个数:");
16 String str=br.readLine();
17 int m=Integer.parseInt(str);
18 intrl.Test(m);
19
}
20 public void Test(int m)
21 {
22 String[] result=new String[m];
23 for(int i=0;i<m;i++)
24 {
25 try
26 {
27 BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
28 System.out.println("总测试例个数为"+m+",现请输入第"+(i+1)+"个用例，数据由三行组成:");
29 String str1=br.readLine();
30 String[] str2=str1.split(" ");
31 double d1=Double.parseDouble(str2[0]);
32 double c=Double.parseDouble(str2[1]);
33 double d2=Double.parseDouble(str2[2]);
34 int n=Integer.parseInt(str2[3]);
35 String str3=br.readLine();
36 String[] str4=str3.split(" ");
37 double[] d=new double[n+1];
38 for(int j=0;j<n;j++)
39 {
40 d[j]=Double.parseDouble(str4[j]);
41 }
42 d[n]=d1;
43 String str5=br.readLine();
44 String[] str6=str5.split(" ");
45 double[] p=new double[n+1];
46 for(int k=0;k<n;k++)
47 {
48 p[k]=Double.parseDouble(str6[k]);
49 }
50 p[n]=0;
51 if(isSolution(c,d2,n,d))
52 {
53 double res=TX(d1,c,d2,n,d,p);
54 result[i]= String.valueOf(res);
55 }
56 else
57 {
58 result[i]= "No Solution";
59 }
60 }
61 catch(IOException e)
62 {
63 System.out.println(e);
64 }
65 }
66 System.out.println();
67 System.out.println("结果：");
68 for(int l=0;l<m;l++)
69 {
70 System.out.println(result[l]);
71 }
72 }
73
74 public boolean isSolution(double c,double d2,int n,double[] d)
75 {
76 for(int i=0;i<n;i++)
77 {
78 if(d[i+1]-d[i]>c*d2)
79 {
80 return false;
81 }
82 }
83 return true;
84 }
85 //d[0]=0;d[n]=d1; p[n]=0;
86 public double TX(double d1,double c,double d2,int n,double[] d,double[] p)/*核心算法*/
87 {
88 double result=0;
89 double[] sy=new double[n+1];
90 double[] x=new double[n];
91 for(int i=0;i<n;i++)
92 {
93 //k指向下一站
94 int k=i+1;
95 //k指向油价比第i站便宜
96 while(p[k]>p[i]&&k<n)
97 {
98 k++;
99 }
100 //如果k站和i站之间距离大于装满油时所能行驶的距离,则加满油
101 if(d[k]-d[i]>c*d2)
102 {
103 x[i]=c-sy[i];
104 }
105 //如果k站和i站之间距离不大于装满油时所能行驶的距离，则保证所加油量只行驶到第k站，并跳过检查其间的加油站是否需要加油
106 else
107 {
108 //若油量足够行驶到k站则不加油
109 x[i]=((d[k]-d[i])/d2>sy[i])?((d[k]-d[i])/d2-sy[i]):0;
110 i=k-1;
111 }
112 sy[i+1]=sy[i]+x[i]-(d[i+1]-d[i])/d2;
113 result+=x[i]*p[i];
114 }
115 return result;
116 }
117}
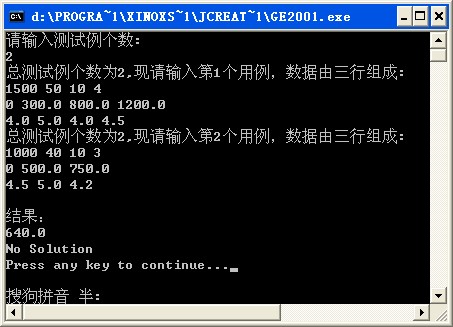
6、运行结果
