1.问题描述
设B是一个n×n棋盘，n=2k,(k=1,2,3,…)。用分治法设计一个算法，使得：用若干个L型条块可以覆盖住B的除一个特殊方格外的所有方格。其中，一个L型条块可以覆盖3个方格。且任意两个L型条块不能重叠覆盖棋盘。
例如：如果n=2，则存在4个方格，其中，除一个方格外，其余3个方格可被一L型条块覆盖；当n=4时，则存在16个方格，其中，除一个方格外，其余15个方格被5个L型条块覆盖。
2. 具体要求
输入一个正整数n，表示棋盘的大小是n*n的。输出一个被L型条块覆盖的n*n棋盘。该棋盘除一个方格外，其余各方格都被L型条块覆盖住。为区别出各个方格是被哪个L型条块所覆盖，每个L型条块用不同的数字或颜色、标记表示。
3. 测试数据
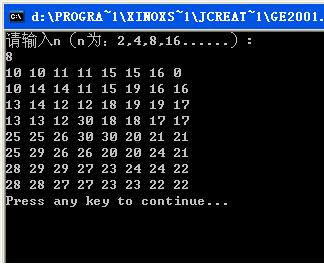
输入：8
输出：
4. 设计与实现的提示
对2k×2k的棋盘可以划分成若干块，每块棋盘是原棋盘的子棋盘或者可以转化成原棋盘的子棋盘。
注意：特殊方格的位置是任意的。而且，L型条块是可以旋转放置的。为了区分出棋盘上的方格被不同的L型条块所覆盖，每个L型条块可以用不同的数字、颜色等来标记区分。
可以采用可视化界面用不同颜色来表示各L型条块，显示其覆盖棋盘的情况。输出有多种表示方式。
5、程序实现（java）
1
import java.io.*;
2public class Ex3_1
3
{
4
static int k=10;
5 public static void main(String[] args) throws Exception
6
{
7 BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
8 System.out.println("请输入n（n为：2,4,8,16）:");
9 String str=br.readLine();
10 int m=Integer.parseInt(str);
11 L(m,2);
12
}
13 public static void L(int m,int n)//n=2,4,8,16
14 {
15 int[][] nn=new int[m][m];
16 l(nn,0,m-1,0,m-1,n);
17 for(int i = 0;i < m;i++)
18 {
19 for(int j = 0;j < m;j++)
20 {
21 System.out.print(nn[i][j]+" ");
22 }
23 System.out.println();
24 }
25 }
26 public static void l(int[][] nn,int x0,int x1,int y0,int y1,int flag)
27 {
28 if((1 == flag)&&(x1>x0)&&(y1>y0))
29 {
30 l(nn,x0,(x1+x0)/2,y0,(y1+y0)/2,1); //1
31 l(nn,x0,(x1+x0)/2,(y1+y0)/2+1,y1,4);//4
32 l(nn,(x1+x0)/2+1,x1,(y1+y0)/2+1,y1,1);//1
33 l(nn,(x1+x0)/2+1,x1,y0,(y1+y0)/2,2);//2
34
35 nn[(x1+x0)/2][(y1+y0)/2+1] = k;
36 nn[(x1+x0)/2+1][(y1+y0)/2+1] = k;
37 nn[(x1+x0)/2+1][(y1+y0)/2] = k;
38 k++;
39 }
40 if((2 == flag)&&(x1>x0)&&(y1>y0))
41 {
42 l(nn,x0,(x1+x0)/2,y0,(y1+y0)/2,3); //3
43 l(nn,x0,(x1+x0)/2,(y1+y0)/2+1,y1,2);//2
44 l(nn,(x1+x0)/2+1,x1,(y1+y0)/2+1,y1,1);//1
45 l(nn,(x1+x0)/2+1,x1,y0,(y1+y0)/2,2);//2
46
47 nn[(x1+x0)/2][(y1+y0)/2] = k;
48 nn[(x1+x0)/2+1][(y1+y0)/2] = k;
49 nn[(x1+x0)/2+1][(y1+y0)/2+1] = k;
50 k++;
51 }
52 if((3 == flag)&&(x1>x0)&&(y1>y0))
53 {
54 l(nn,x0,(x1+x0)/2,y0,(y1+y0)/2,3); //3
55 l(nn,x0,(x1+x0)/2,(y1+y0)/2+1,y1,4);//4
56 l(nn,(x1+x0)/2+1,x1,(y1+y0)/2+1,y1,3);//3
57 l(nn,(x1+x0)/2+1,x1,y0,(y1+y0)/2,2);;//2
58
59 nn[(x1+x0)/2][(y1+y0)/2] = k;
60 nn[(x1+x0)/2+1][(y1+y0)/2] = k;
61 nn[(x1+x0)/2][(y1+y0)/2+1] = k;
62 k++;
63
64
65 }
66 if((4 == flag)&&(x1>x0)&&(y1>y0))
67 {
68 l(nn,x0,(x1+x0)/2,y0,(y1+y0)/2,3); //3
69 l(nn,x0,(x1+x0)/2,(y1+y0)/2+1,y1,4);//4
70 l(nn,(x1+x0)/2+1,x1,(y1+y0)/2+1,y1,1);//1
71 l(nn,(x1+x0)/2+1,x1,y0,(y1+y0)/2,4);//4
72
73 nn[(x1+x0)/2][(y1+y0)/2] = k;
74 nn[(x1+x0)/2][(y1+y0)/2+1] = k;
75 nn[(x1+x0)/2+1][(y1+y0)/2+1] = k;
76 k++;
77 }
78 }
79
}
6、运行结果
